Changed on 26/02/2020
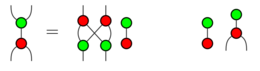
Intitulé « A near optimal axiomatisation of ZX Calculus for Pure Quantum Mechanics », l’article propose un certain nombre d’équations qui axiomatisent la mécanique quantique. Le langage ZX Calcul permet de représenter une évolution quantique avec des diagrammes, de la même façon qu’un circuit classique représente une fonction booléenne. Ceci permet d’éviter d’utiliser les espaces de Hilbert, employés dans le formalisme quantique habituel. « Le diagramme est en effet plus parlant, plus graphique que l’élément de l’espace de Hilbert associé. Il offre une vision plus simplifiée mais toujours formelle et permet de visualiser où sont les qbits et de schématiser certaines équations », ajoute le jeune lauréat. C’est la théorie des catégories qui assure la cohérence entre une formule mathématique et un diagramme.
Qu’est ce qu’un qbit ?
Un qbit, prononcé « qubit », est l’état quantique qui représente la plus petite unité de stockage d’information quantique. C’est l’analogue quantique du bit, les effets quantiques apparaissant à l’échelle de l’atome. Les bits classiques ne peuvent être que dans deux états : soit « 0 », soit « 1 ». Le qbit, lui, est une combinaison linéaire de ces deux états, et est représentable par le langage ZX Calcul. Des applications relativement concrètes existent, telles que l’analyse d’algorithme ou de circuit. On peut également utiliser le ZX Calcul à des fins de vérifications de protocole, et ce sans ordinateur quantique.
À quoi sert un ordinateur quantique ?
L’ordinateur quantique dispose d’une plus grande puissance de calcul qu’un ordinateur classique. Le meilleur exemple est l’algorithme de Shor qui permet de factoriser efficacement un nombre en nombres premiers, problème considéré difficile pour un ordinateur classique. Si les ordinateurs quantiques existent déjà, ils restent très petits, i.e. le nombre de qbits est lui-même très petit. En effet, plus le système est gros, plus il est difficile de lui faire garder ses propriétés quantiques.
La théorie quantique peut être capturée par des axiomes sur les portes logiques qui constituent un circuit quantique. C’est une alternative viable au calcul quantique dans les espaces de Hilbert, espaces qui permettent de mesurer des longueurs et des angles. Le langage quantique ZX Calcul donne un ensemble d’axiomes qui capturent la mécanique quantique, le but recherché étant que toute transformation qui devrait être permise est bel et bien dérivable d’après les axiomes. Et c’est l’objet même de l’article récompensé. Une forte communauté de logiciens travaille déjà sur ce langage, notamment à Oxford, Nijmegen et Grenoble.
Que diriez-vous à des étudiants qui souhaiteraient préparer une thèse ?
« Je leur dirais que l’environnement de travail est génial et réunit toutes les conditions pour mener à bien sa thèse. J’ai choisi ce métier et ce sujet car l’environnement est stimulant et bouillonnant et il permet la reconnaissance de son travail à travers le monde. »
Renaud Vilmart a étudié à Mines Nancy et c’est un cours de Simon Perdrix sur l’informatique quantique qui a convaincu Renaud de se diriger vers cette thématique de recherche pour sa thèse. Aujourd’hui en 3e année, il prévoit de soutenir sa thèse à la rentrée et de réaliser un postdoctorat.