Xavier Pennec, virtuose de la statistique géométrique au service de la santé
Date:
Mis à jour le 22/10/2024
Le principe : nous partons d’un objet qui semble être dans un espace euclidien "classique", mais lorsque nous voulons effectuer une analyse qui ne dépende ni de sa position, ni de son orientation dans l'espace, la géométrie est nécessaire. Mon travail consiste à redéfinir les notions statistiques habituelles pour qu’elles fonctionnent proprement sur ces espaces géométriques.
Nous pouvons ensuite modéliser des données en sciences de la vie, en particulier pour analyser la variabilité biologique de la forme des organes au cours du temps. C’est ce qu’on appelle l’anatomie computationnelle, une discipline émergente à la croisée de la géométrie, des statistiques, de l'analyse d'images et de la médecine.
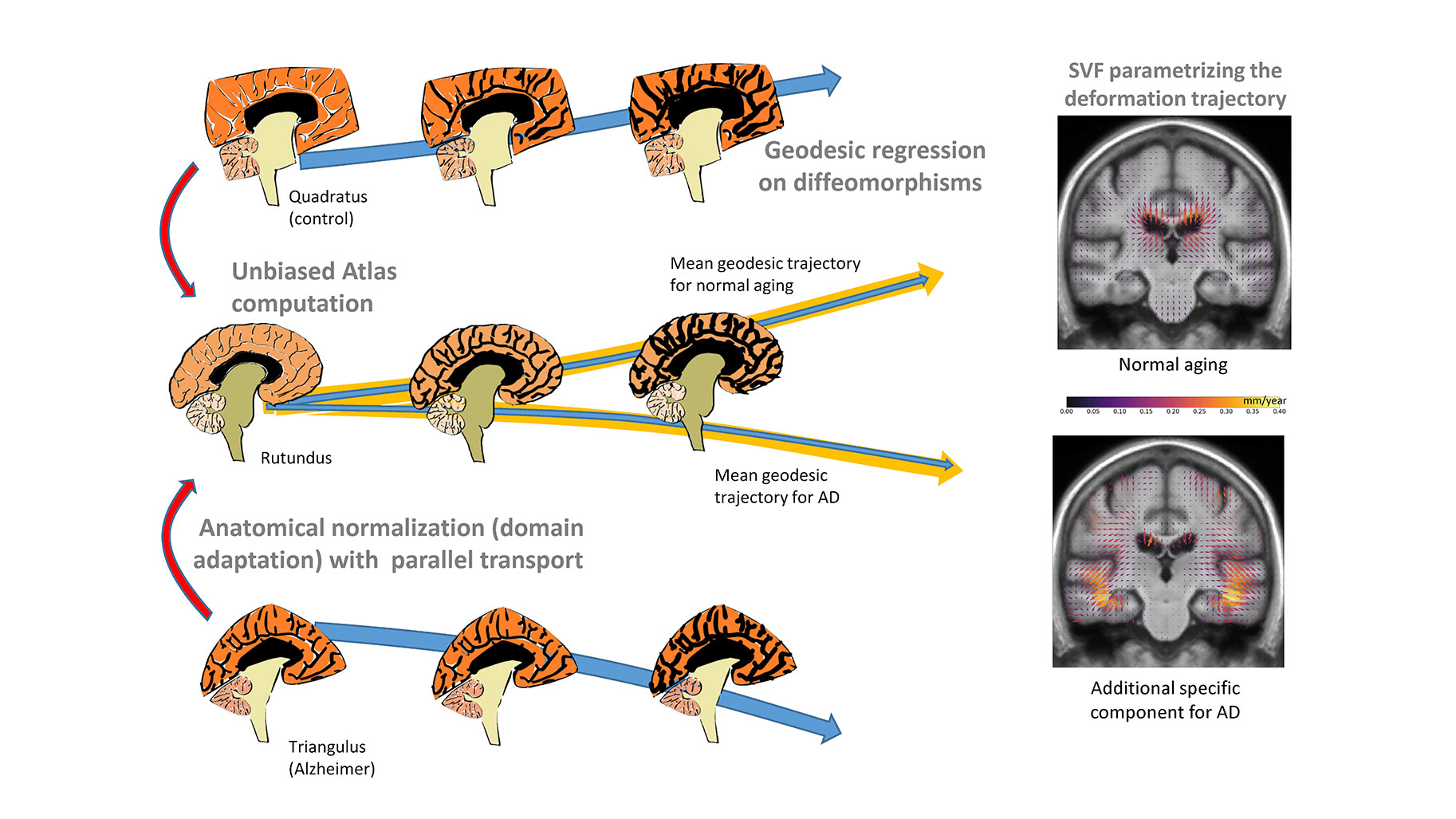
Dans les années 1990, pour étudier deux cerveaux, on analysait les points communs et les différences des images après les avoir superposées au mieux par rotation et translation, une méthode capitale pour l'imagerie médicale qu’on appelle le recalage. Dans les années 2000, les méthodes ont évolué pour passer à des recalages par déformations, qui permettent de superposer les images presque parfaitement. On a alors transféré l’analyse statistique des similarités et des différences de l’image vers les transformations elles-mêmes. Mais pour observer ces déformations de dimension infinie de manière stable, il a fallu identifier les structures géométriques sous-jacentes à respecter pour rajouter suffisamment de contraintes. Par exemple, la structure de groupe de difféomorphisme fournit un moyen de mieux modéliser les déformations, tout en garantissant les propriétés de l'objet grâce aux statistiques géométriques.
Dans la communauté scientifique MICCAI (Medical Image Computing and Computer Assisted Intervention), tous les professionnels de la médecine ont compris l'intérêt de ces méthodes et se sont impliqués en leur faveur. Car celles-ci permettent de mieux prédire et contrôler la variabilité biologique.
Par exemple, nous l’avons utilisé pour étudier les cerveaux de personnes atteintes de la maladie d'Alzheimer. Nous disposions d’images collectées à un an d’intervalle et nous avons estimé la déformation sur cette durée pour chaque sujet. Il nous a aussi fallu comparer les sujets entre eux, ce qui nécessite une méthode pour adapter la déformation de chacun. Grâce à la géométrie, nous avons pu établir une trajectoire de déformation moyenne à partir d’une anatomie de référence, modélisée par une géodésique dans l’espace des déformations, une notion qui généralise la ligne droite dans un espace courbe. Puis, nous avons extrapolé le long de la géodésique, afin de modéliser l’évolution du cerveau sept ans avant et sept ans après. Nous pouvons ainsi comparer un cerveau jeune à un cerveau très âgé atteint d'Alzheimer. Notre modélisation continue à ressembler à un cerveau plausible, sans aberration évidente. Nous ne sommes pas exactement conformes à la réalité, mais nous nous en approchons.
Nous avons aussi utilisé ces techniques pour des études sur la scoliose : nous avons modélisé les variabilités de toutes les vertèbres, les unes par rapport aux autres. En observant notre moyenne, nous avons pu ainsi reconstruire une colonne vertébrale "moyenne". Mais surtout, nous avons pu visualiser les variations les plus typiques et les comprendre anatomiquement. Nos modèles statistiques permettent donc la description et la prédiction, tout en améliorant l’interprétation.
Notre difficulté, c'est que nous observons des éléments du vivant, soumis à une variabilité extrême. Et ce que nous visons, c'est la structure minimale qui nous permet d'approcher au mieux la géométrie de toutes les données. Certes, sur le plan statistique, nos modèles très simples ne sont pas exacts, mais l'important est qu'ils soient suffisamment explicatifs et prédictifs.
En sciences de la vie, nos approximations peuvent apporter énormément d'informations aux endroits où l’on manque de données. Dans le domaine médical, les scientifiques étudient parfois uniquement une pathologie, ou une sous-pathologie bien précise, avec à peine 10 ou 100 données à leur disposition, ce qui est très faible. La géométrie peut apporter l’information a priori manquante pour à la fois décrire correctement les données et interpoler de manière plausible entre celles-ci pour mieux estimer ou prédire.
C'est l’un des financements les plus intéressants pour la recherche fondamentale. Car grâce à ce soutien, nous pouvons penser loin et proposer des sujets qui n'ont pas encore d'applications concrètes. Ce recul permet de concevoir de nouvelles façons d’aborder les problèmes auxquels on ne peut pas penser quand on reste trop près des problèmes pratiques. C’est ainsi que beaucoup de percées scientifiques ont été réalisées, avec à la clé des applications radicalement nouvelles qui ont été développées bien plus tard.
J'ai ainsi pu recruter toute une équipe dédiée et construire un cadre mathématique rigoureux autour des statistiques géométriques, pour savoir ce qui fonctionne, dans quel contexte, etc. Désormais, avec cette connaissance acquise pendant cinq ans de recherches plus théoriques, mon équipe et moi pouvons revenir aux données et aux applications avec plus de pertinence. Aujourd’hui, nous développons des méthodologies nouvelles et nous identifions les limites de ce que nous pouvons obtenir. Et il existe encore de nouveaux territoires à explorer grâce à cette vision géométrique !

Directeur de recherche, équipe Epione
2004, route des Lucioles
,
06560 Valbonne Sophia Antipolis